Transformers are well-known for their ability to generate text and images, but are they applicable to other use cases? In this post, we will explore how to adapt the transformer neural network architecture to produce solutions to a range of routing problems. We will first survey current research on the topic and then dive into the details of how to implement a transformer-based model for a custom variant that represents a real-world scenario. Finally, we will evaluate the model's performance and discuss potential improvements.
Contents
- Deep learning and combinatorial optimization
- Vehicle Routing Problems (VRP)
- Solving VRPs (up until now)
- Deep learning to the rescue
- Digging deeper: adapting transformers for VRPs
- Promising experimental results
- Let's give it a try!
Deep learning and combinatorial optimization
Research on neural network-driven methods for solving combinatorial optimization problems has seen an increased interest for a few good reasons:
- Some combinatorial optimization problems are NP-Hard: algorithms that search in their solution space have exponential time complexity. This makes them hard to solve for large instances. Most state-of-the-art solvers nowadays are based on heuristics and approximation methods used to reduce the search space, but they are not guaranteed to find the optimal solution.
- Reliable and scalable algorithms to such problems are crucial for many practical applications in several key industries, such as logistics, transportation, and telecommunications. For instance, the Traveling Salesman Problem (TSP) finds applications in vehicle routing, circuit design, and DNA sequencing.
- Deep learning models have recently shown promising results in solving combinatorial optimization problems, thanks to breakthroughs in reinforcement learning and attention mechanisms (e.g., transformers).
Vehicle Routing Problems (VRP)
With research dating back to the 1950s, Vehicle Routing Problems have been popular in the field of combinatorial optimization. The basic premise is the following: an agent must visit a set of nodes or edges in a specific order while fulfilling a set of constraints and optimizing a set of variables. In common variants, this often translates to a fleet of vehicles that must deliver goods to a set of customers while minimizing the total distance traveled or the total time spent.
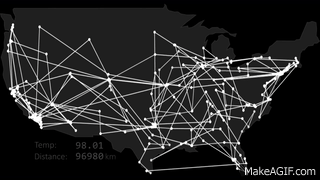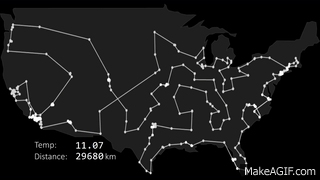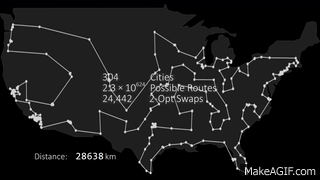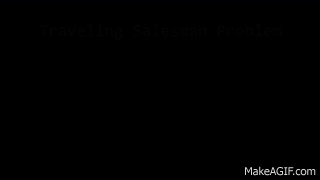
In reality, VRPs can get quite complex. For instance, the Capacitated Vehicle Routing Problem (CVRP) adds the constraint that each vehicle has a limited capacity and can only deliver a certain amount of goods. The Multiple Depot Vehicle Routing Problem (MDVRP) extends the problem to multiple depots, each with its own fleet of vehicles. The Pickup and Delivery Problem (PDP) adds the constraint that each vehicle must pick up goods from one location and deliver them to another. The Capacitated Vehicle Routing Problem with Time Windows, Unmatched pickups and deliveries, Priority tasks, and Inventory restrictions (CVRPTWUPI) adds... well, you get the idea, the list goes on...
Solving VRPs (up until now)
Like mentioned earlier, solving combinatorial optimization problems is no easy task, and VRPs are no exception. The most common approach is to use heuristics and approximation methods, though recent research has yielded myriad other methods, from ant colony optimization to deep-q learning. The extent of research on the topic is summarized in the diagram below:
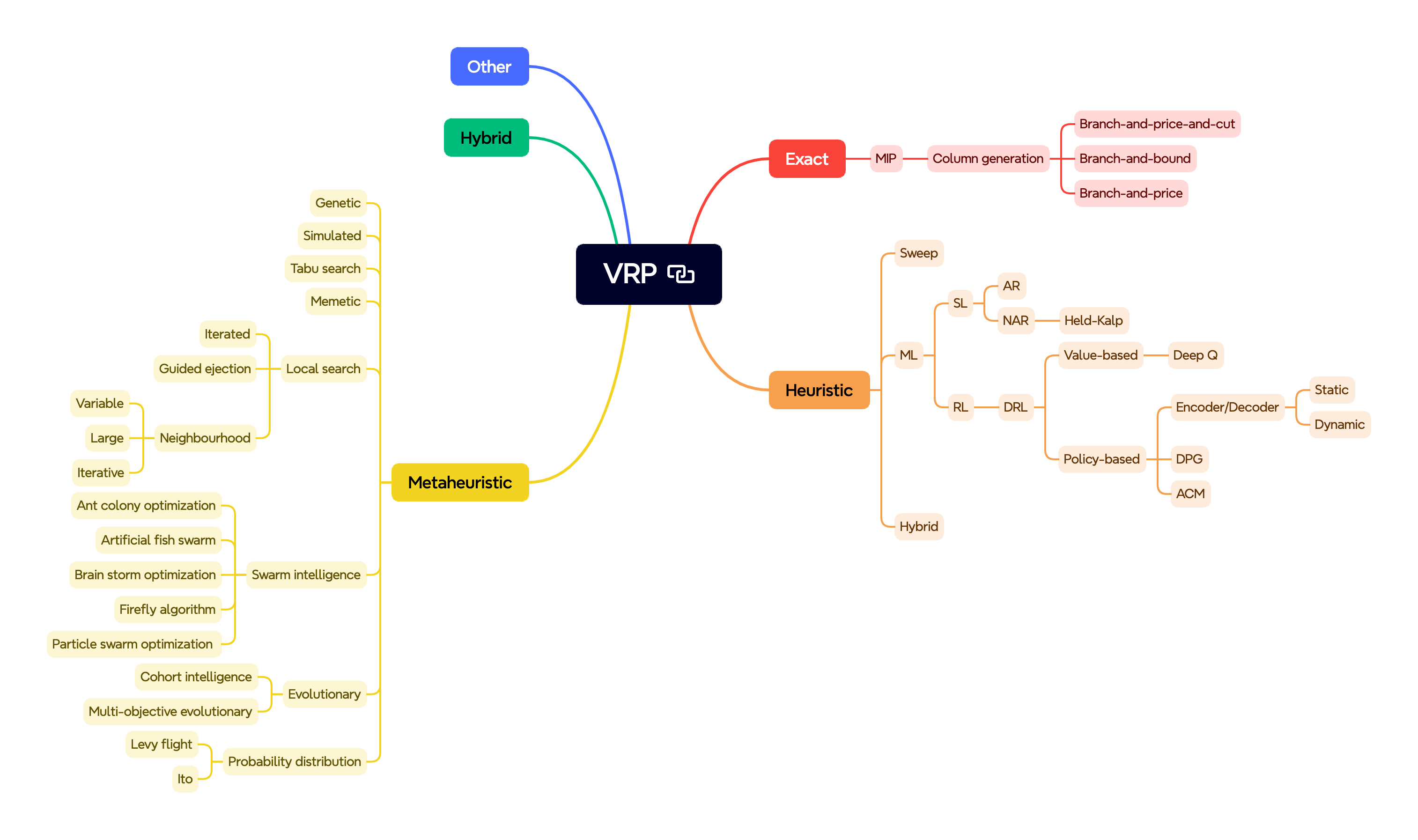
The common point of contention these methods aim to address is the significant so-called "expert intuition" required to generate solutions. Take the example of Concorde - a state-of-the-art solver considered the fastest for large instances of the TSP. Concorde leverages 50 years of research and development in the field of combinatorial optimization, and it is still not guaranteed to find the optimal solution for more than a few hundred nodes. Let us remember that the TSP is a relatively simple variant of the VRP.
Deep learning to the rescue
Beyond reasons aforementioned, deep learning presents multitple advantages over traditional methods for solving VRPs:
- Neural networks can be trained to generalize solutions to previously unseen instances, making them more adaptable to a broad range of scenarios.
- Doing so does not require handcrafting heuristics or approximation methods, which can be time-consuming and error-prone.
- Neural networks can leverage the power of GPUs and TPUs to parallelize computations, lending themselves to faster training and inference, potentially enabling real-time routing solutions.
- As we will see later, deep learning models can be spun up to solve very specific variants of VRPs with minimal modifications, making them a great resource to explore understudied or novel problems.
It turns out that so-called "neural combinatorial optimization" solvers have been found to follow a general pipeline:
Out of those steps, graph embedding is the most interesting to consider in detail, the reason being that other components remain relatively unchanged across different problems. Graph embedding consists in transforming a graph into a vector representation that can be subsequently fed to neural networks. This representation aims to capture the essential information about the graph's structure and properties, such as the nodes, edges, and their attributes (capacities, time windows, etc.).
Digging deeper: adapting transformers for VRPs
When it comes to embeddings, recent advances in attention mechanisms have recently pushed transformers to the top of the list of potential neural network architectures for solving VRPs. Transformers can capture long-range dependencies in the graph, which is crucial for routing problems where the order of nodes matters. The transformer architecture consists of an encoder-decoder pair, each composed of multiple layers of multi-head self-attention and feed-forward neural networks. The encoder processes the input graph, while the decoder generates the output sequence of nodes to visit. The transformer's attention mechanism allows it to focus on different parts of the graph, making it well-suited for routing problems.
Adapting the positional encoding
One of the key components of the transformer architecture is the positional encoding, which allows the model to distinguish between nodes based on their position in the graph. Much like when processing text, the order in which token or nodes appear is crucial for the model to generate meaningful outputs. The original transformer encoder adds a position-dependent signal based on sine and cosine functions to each token embedding to help the model incorporate the relative position of tokens in the input sequence (see figure (a) below).
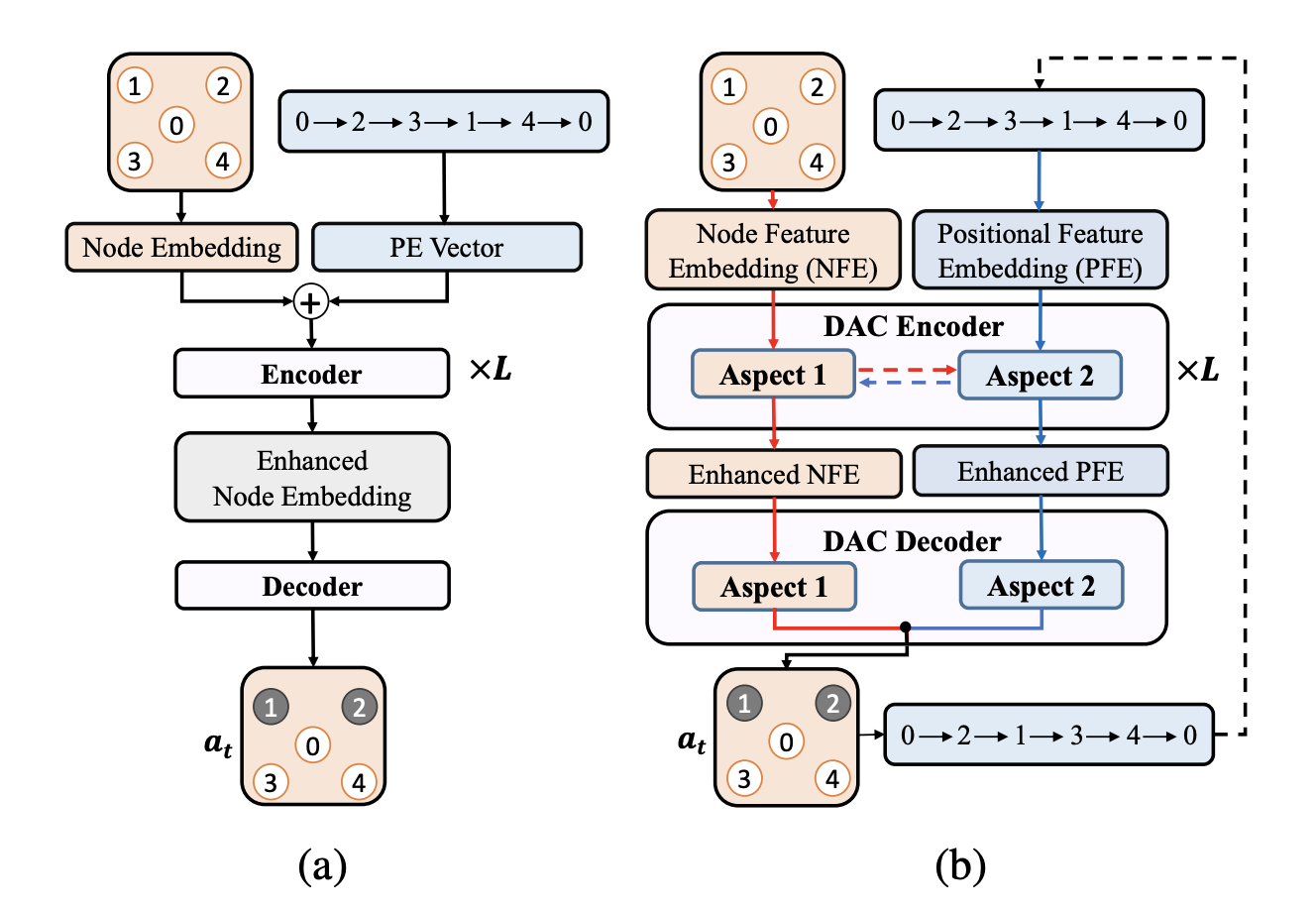Nonetheless, VRPs are different from text in a few key ways:
- Most VRPs are cyclical by nature: vehicles must return to their starting point after visiting all nodes. Encoding linear sequences could impede the model's ability to learn the cyclical nature of the problem, leading to suboptimal solutions.
- VRP nodes carry additional attributes: in addition to their position in the graph, nodes may have other properties such as demand, time windows, and service times. These attributes are crucial for the model to generate feasible solutions. The transformer's embedding must be able to capture these properties effectively.
- Positional attributes are non-deterministic: in contrast to text, where the order of tokens is statistically significant, the order of nodes in a VRP is arbitrary. The model must be able to learn the importance of each node based on its attributes, rather than its position in the sequence.
- VRP node attributes are non-additive and non-linear: the model must be able to capture complex relationships between node attributes, such as the capacity constraints of vehicles or the time windows of nodes. A simple linear or additive embedding may not be sufficient to represent these relationships.
A revised architecture can be see in figure (b) above, where a so-called "dual-aspect" encoder separates Node Feature Embeddings (NFEs) from Positional Feature Embeddings (PFEs). Notably, PFEs can be generated using a learned embedding, rather than a fixed positional encoding, allowing the model to learn the importance of each node based on its attributes. Another possiblity is to use cyclical positional encodings based on cyclic Gray codes or other cyclical functions to capture the cyclical nature of VRPs.
Cross-aspect attention
With two distinct sets of embeddings (NFEs and PFEs), the model must be able to attend to both aspects of the input graph simultaneously. Cross-aspect attention mechanisms enable the model to leverage correlations between node attributes and positions, sharing knowledge between each aspect to achieve a synergy. Specifically, the cross-aspect attention mechanism can be implemented by concatenating NFEs and PFEs and feeding them to the multi-head self-attention layers of the transformer encoder.
Promising experimental results
Various publications on the topic have shown promising results, with transformer-based models achieving results comparable to state-of-the-art solvers such as OR-Tools, though suffering from slow inference times with large problem instances (500+ nodes) due to a lack of heuristic search optimizations. Nonetheless, as expected the models have shown to generalize well to unseen instances and can be trained on a variety of VRP variants with minimal modifications (demonstrated on TSP and CVRP variants).
In the future, we can expect further research to focus on improving the scalability and efficiency of such modes, potentially by exploring compression techniques, parallelization strategies, and hybrid models that combine neural networks with traditional solvers. Additionally, the field is ripe for exploration of novel VRP variants and real-world applications, such as dynamic VRPs, stochastic VRPs, and multi-objective VRPs. The potential for transformers to revolutionize the field of combinatorial optimization is vast, and we are only beginning to scratch the surface of what is possible!
Let's give it a try!
To demonstrate the methods described above, we will benchmark Ma et al's transformer-based model on a set of 100 baseline VRP instances with 100 nodes each. The model is loaded from the provided checkpoints and evaluated versus a state-of-the-art solver (Hexaly) on the same instances. The results are summarized in the table below:
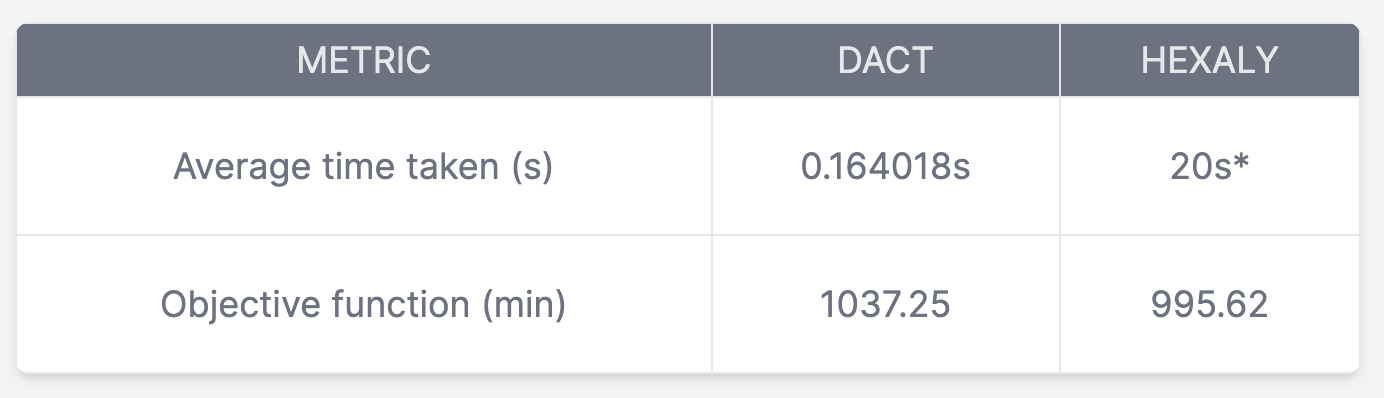*Hexaly's search was is capped at 20s.
Interestingly, the transformer managed to obtain decent results with an extremely small inference time. Not bad! Here is a solution generated by the transformer model, visualized with VRPTK:
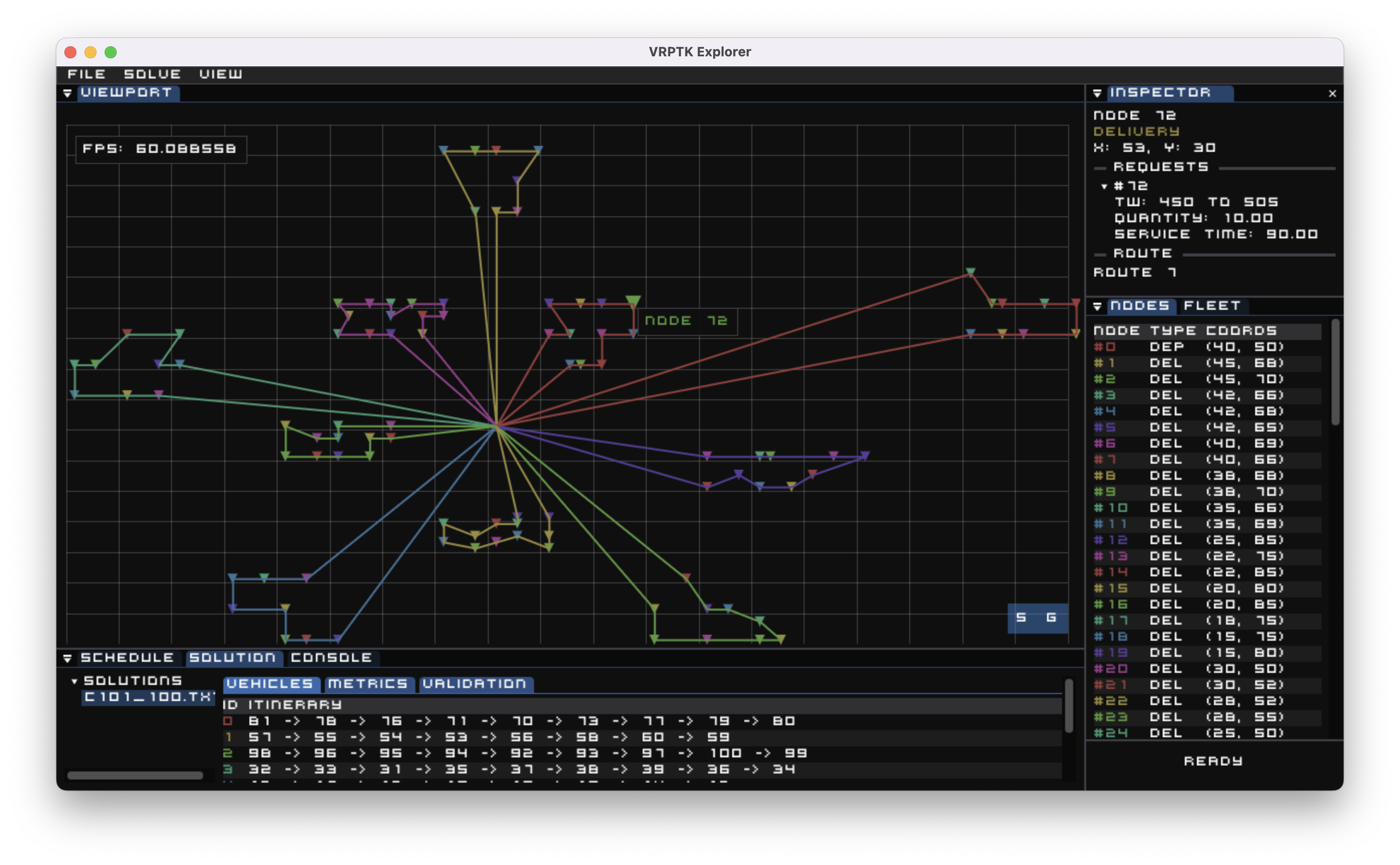
Code for the model can be found here.
Many thanks to Professor Antoine Desir for his guidance and insights on the topic.